Algorithmes élémentaires de tri, applications, et recherche dichotomique

Table des matières

1. Implémentation d'un algorithme de tri
2. Utilisation d'une liste triée
3. Recherche dichotomique dans un tableau trié
4. Exercices
- 4.1. Sur les tris
- 4.2. Recherche dichotomique
  - d'un zéro d'une fonction continue

1. Implémentation d'un algorithme de tri

Étant donné une liste de nombres, on veut réordonner ses éléments par ordre croissant, soit en modifiant la liste, soit en créant une nouvelle liste.

1.1. Tri par sélection

Étant donné une liste l, écrire du code Python qui détermine l'indice d'un minimum de la liste, et place ce minimum au début de la liste l, en échangeant sa position avec celle du premier élément de la liste.
Écrire une fonction tri_sel qui trie une liste en argument. On commencera par sélectionner le minimum de la liste et échanger sa position avec le premier élément de la liste, puis on recommencera avec les éléments à partir du second, etc.
On note $n$ la taille de la liste. Quel est le nombre de comparaisons effectuées par cet algorithme ?
En utilisant la fonction tri_sel précédente, écrire une fonction tri_sel_pur qui prend en argument une liste, et renvoie une nouvelle liste, triée. La fonction tri_sel_pur ne doit pas avoir d'effet de bords (elle ne doit pas modifier la liste en argument).

On dit que la complexité de l'algorithme est quadratique, ou en $O(n^2)$ : il existe une constante $C$ telle que le nombre d'opérations soit inférieur à $C n^2$, où $n$ est la longueur de la liste.

1.2. Tri par propagation

Justifier la correction de l'implémentation ci-contre d'un algorithme de tri. On énoncera en particulier un invariant de la boucle extérieure sur i, sous la forme d'une assertion «après l'itération d'indice i de la boucle extérieure, la liste l vérifie telle propriété.»

def tri_prop(l):
    n = len(l)
    for i in range(n):
        for j in range(n-i-1):
            if l[j] > l[j+1]:
                l[j], l[j+1] = l[j+1], l[j]

1.3. Tri par positionnement

Écrire une fonction tri_pos qui prend en argument une liste l et qui renvoie une nouvelle liste, contenant les mêmes éléments que l, mais triés par ordre croissant. On supposera que la liste en argument ne contient aucun doublon (que tous ses éléments soient distincts).

On commencera par créer une liste de même taille que l contenant des $0$, puis, pour chaque élément de l, on comptera le nombre d'éléments de l qui lui sont inférieurs avant de placer cet élément dans la liste créée, à la bonne position.
★ Réécrire la fonction précédente, de sorte qu'elle fonctionne encore si la liste en argument a des doublons.

On pourra initialiser la liste à renvoyer avec des valeurs None plutôt que $0$, via l'instruction l = [None] * n.

Cet algorithme de tri a également une complexité quadratique en la longueur de la liste.

1.4. Tris rapides

On verra plus tard des tris «rapides» comme le tri fusion, et le tri pivot, qui ont des complexités en $O(n\ln n)$ dans le pire des cas pour le premier, et en moyenne pour le second.

La complexité d'un algorithme de tri «rapide» est en $\boxed{O(n\ln n)}$.

On peut par ailleurs montrer que c'est en un sens la complexité optimale d'un algorithme de tri générique.

1.5. Tri par comptage stable, et tri par base

On veut trier une liste d'entiers positifs, que l'on suppose pas trop grands.

Écrire une fonction chiffre qui prend en argument un entier positif $n$ et un indice $i\in\N$ et renvoie le chiffre décimal d'indice $i$ de $n$. Par exemple chiffre(123, 0) renvoie $3$, et chiffre(123, 1) renvoie $2$.
Écrire une fonction tri_comptage_chiffre qui prend en argument une liste l d'entiers positifs, et un indice $i$ et trie la liste selon les chiffres d'indice $i$ de ses éléments.

Par exemple, pour l = [17, 123, 1110, 39, 26] et $i = 0$, on modifiera la liste en [1110, 123, 26, 17, 39].

On veut que le tri effectué soit stable, c'est-à-dire que si deux entiers ont le même chiffre, ils soient positionnés l'un par rapport à l'autre comme dans la liste initiale.

On procédera par comptage : pour chaque chiffre possible, on comptera le nombre d'éléments de l ayant ce chiffre.
Justifier que la fonction suivante trie sa liste en argument. Quelle est sa complexité, en fonction de $n = \texttt{len(l)}$ et $\om = \texttt{log}$ ?

def tri_base(l):
    log = max([math.floor(math.log10(e)) for e in l]) # le maximum des ℓfloor ℓog e⌋, pour e dans l
    for i in range(log + 1):
        tri_comptage_chiffre(l, i) # On trie les éléments de l, suivant leurs i-ème chiffre

2. Utilisation d'une liste triée

2.1. Algorithmes de tri de `Python`

Python met à disposition des fonction et méthode implémentant des tris rapides. On peut utiliser

la fonction sorted qui prend une liste en argument et renvoie une nouvelle liste, contenant les mêmes éléments, mais triés.
la méthode sort, qui trie une liste donnée (donc la modifie).

In [1]: l = [3,6,2,1]
In [2]: l.sort()
In [3]: l
Out[3]: [1,2,3,6]

In [1]: l = [3,6,2,1]
In [2]: lb = sorted(l); lb
Out[2]: [1,2,3,6]
In [3]: l
Out[3]: [3,6,2,1]

En particulier, la complexité des implémentations de Python est en $O(n\ln n)$, meilleure que quadratique.

On peut utiliser ces fonctions pour trier

une liste de chaîne de caractères, selon l'ordre du dictionnaire

assert(sorted(["babar", "ana", "ceci"]) == ["ana", "babar", "ceci"])
une liste de couples, selon l'ordre lexicographique

assert(sorted([(2,4), (1,3), (1,-2)]) == [(1,-2), (1,3), (2,4)])
les lettres d'une chaîne de caractères

assert(sorted("babar") == ["a", "a", "b", "b", "r"])

2.2. Exercices

Dans les exercices suivant, on utilisera les méthode et fonction sort et sorted de Python.

Écrire une fonction mediane qui prend en argument une liste d'entiers et qui renvoie une médiane de cette liste, c'est-à-dire un élément $m$ de la liste, tel qu'au moins la moitié des éléments de l soit $\geq m$, et qu'au moins la moitié des éléments de l soit $\leq m$.

Écrire une fonction contient_doublon qui prend en argument une liste d'entiers et qui renvoie True si la liste admet des doublons (si elle contient plusieurs fois le même élément). L'objectif est d'avoir une complexité meilleure que quadratique.

Écrire une fonction nb_elem_distinct qui prend en argument une liste d'entiers et qui renvoie le nombre d'éléments distincts de cette liste.

Écrire une fonction tri_dec qui prend en argument une liste d'entiers et qui modifie cette liste, en la triant par ordre décroissant. On n'utilisera pas l'argument facultatif reverse de la méthode sort décrit ci-après.

Les fonctions sorted et sort peuvent prendre un paramètre facultatif reverse=True qui permet de trier la liste par ordre décroissant.

Écrire une fonction element_commun qui prend en argument deux listes l1 et l2 et qui renvoie True si les deux listes ont un élément en commun. On proposera une solution de complexité meilleure que quadratique, sans utiliser de mémoire supplémentaire.

2.3. ★ Calcul de l'enveloppe convexe d'un nuage de points, par balayage.

On représente des points de $\R^2$ par des couples de flottants. L'objectif est le calcul de l'enveloppe convexe d'un nuage de points de $\R^2$, représenté par une liste de points.

Écrire une fonction qui prend en argument une liste de points, et renvoie une nouvelle liste, formée de ces mêmes points, mais triée par abscisses croissantes.
Écrire une fonction qui prend en argument les coordonnées de trois points distincts $A,B,C$, et renvoie $1$ si le triangle $ABC$ est orienté positivement, $-1$ négativement, et $0$ si les trois points sont alignés.

Pour calculer l'enveloppe convexe, on procède par balayage. On itère sur les points du nuage, par abscisses croissantes, et on met à jour l'enveloppe convexe des points considérés jusque là.

Pour cela, on maintiendra deux listes différentes, représentant les parties supérieures et inférieures de l'enveloppe convexe, que l'on mettra à jour à chaque fois que l'on considère un nouveau point, selon le principe de l'illustration de droite.

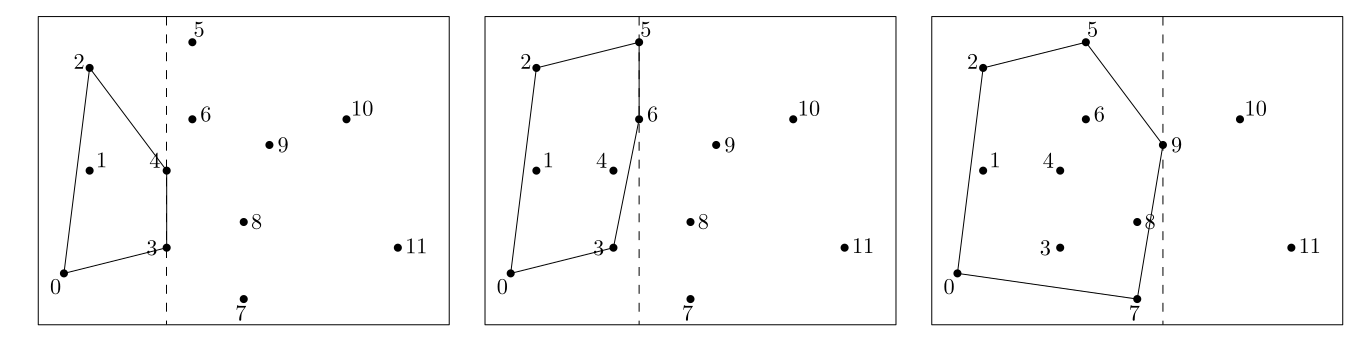
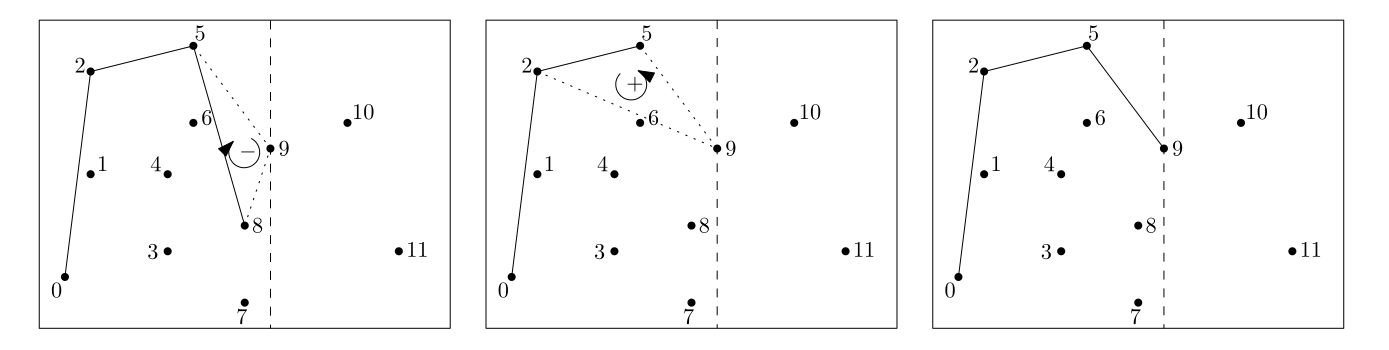
Écrire une fonction qui renvoie l'enveloppe convexe d'un nuage de points, sous la forme de la liste des points de celle-ci. Quelle est la complexité de l'algorithme ?

3. Recherche dichotomique dans un tableau trié

Écrire une fonction recherche_dichotomique qui prend en argument une liste triée l et un élément e et qui décide si l'élément appartient à la liste. On procédera par dichotomie : on commence par comparer l'élément e à un élément du milieu de la liste, et suivant le résultat, on cherche dans la bonne moitié de l, en recommençant.

3.1. L'algorithme

Étant donné un entier e et une liste d'entiers l déjà triée de longueur $n$, on veut décider si la liste l contient l'entier e ou non. La méthode naïve consiste à comparer l'élément e à chaque élément de la liste. Dans le pire des cas, cette méthode nécessite $n$ comparaisons. On dit que sa complexité est linéaire.

Comme la liste est triée, on peut procéder de manière plus efficace. On commence par comparer e à un élément à peu près au milieu de la liste, comme $c_1 = \texttt{l}\left[E(\frac{n-1}{2})\right]$. Si $c_1 \gt e$ par exemple, c'est que e ne peut appartenir qu'à la première moitié de la liste.

On recommence, en comparant e à un élément $c_2$ situé au premier quart de l. Si $c_2 \lt e$ par exemple, c'est que e ne peut appartenir qu'au second quart de la liste, etc.

À chaque étape le nombre d'éléments de l qui peuvent potentiellement être égal à e est divisé par deux (environ). Grossièrement, si $n= 2^m$, après $m$ étapes, il n'y aura plus qu'un seul candidat et on pourra conclure. Au total, l'algorithme aura effectué $m + 1 = \log_2(n) + 1$ comparaisons, au lieu de $n$ comparaisons pour l'algorithme naïf. On dit que sa complexité est logarithmique.

La fonction suivante implémente cet algorithme de recherche dichotomique. Elle prend en argument une liste triée d'entiers l et un entier e, et détermine si l'élément e appartient à la liste.

def recherche_dichotomique(l,e):
    a, b = 0, len(l)-1 # a=0 et b = n−1
    # a et b représentent les extrémités de l'intervalle de la liste
    # dans lequel on cherche l'élément e
    if e > l[b] or e < l[a]:
        return False
    # On a \texttt{l[a]} ≤\texttt{e} ≤\texttt{l[b]}
    while b > a + 1:
        c = (a + b) // 2 # c = ℓfloor \frac{a+b}{2}⌋
        if l[c] < e:
            a = c
        else:
            b = c
        # Dans les deux cas, on a toujours \texttt{l[a]} ≤\texttt{e} ≤\texttt{l[b]}
    # À la sortie de la boucle, on a b≤a+1, donc b=a ou b = a+1
    return e == l[b] or e == l[a]

L'algorithme de recherche dichotomique a une complexité en $O(\ln n)$, où $n$ est la longueur de la liste.

Notons $u_i$ le nombre de positions où l'élément $e$ peut être après la $i$-ème itération de la boucle, avec $u_0 = n$.

Tant que la boucle tourne, on vérifie (cf page suivante) que $\quad\displaystyle u_{i+1} \leq \frac{u_i}{2} + 1$ (en fait $u_{i+1}\leq \frac{u_i}{2} + \frac{1}{2}$).

On peut donc majorer la suite $(u_i)$ par une suite $(v_i)$ vérifiant $v_0 = n$ et $\forall i,\, v_{i+1}= \frac{v_i}{2} + 1$. Mais $\forall i\in\N,\, v_i = \frac{1}{2^i} (v_0 - 2) + 2$.

Alors pour $i\gt \log_2 (n-2)$ on a $\frac{1}{2^i} (n-2) \lt 1$, donc $v_i \lt 3$, donc $u_i \leq 2$.

D'autre part, quand $u_i = 2$, c'est que $b = a+1$, donc la boucle while s'arrête. La boucle while tourne donc au plus $\log_2(n) = \frac{\ln n}{\ln 2}$ fois.

3.2. Quelques variantes…

Parmi les fonctions suivantes, identifier celles qui ne sont pas correctes. Expliquer.

def recherche_dicho1(l,e):
    a, b = 0, len(l)-1
    while a < b:
        c = (a + b) // 2
        if l[c] < e:
            a = c
        else:
            b = c
    return e == l[c]

def recherche_dicho2(l,e):
    a, b = 0, len(l)-1
    while a < b:
        c = (a + b) // 2
        if l[c] < e:
            a = c + 1
        else:
            b = c
    return e == l[c]

def recherche_dicho3(l,e):
    a, b = 0, len(l)-1
    while a < b:
        c = (a + b) / 2
        if l[c] < e:
            a = c + 1
        else:
            b = c
    return e == l[c]

3.3. Étude de correction de l'algorithme diff

3.3.1. Notations

On note $n$ la longueur de l, $a_i,b_i,c_i$ les valeurs des variables a, b, c à l'issue de la $i$−ème itération de la boucle while.

On a donc

$a_0 = 0$, $b_0 = n-1$
pour $i\geq 1$, $c_i = \lfloor \frac{a_{i-1} + b_{i-1}}{2}\rfloor$.
si $\texttt{l}[c_i] < e$, $a_{i} = c_i$ et sinon, $b_{i} = c_i$

3.3.2. Propriétés de la boucle

Tant que la boucle ne s’arrête pas, on a $a_i + 1 \lt b_i$, c'est-à-dire $b_i - a_i \gt 1 \ssi b_i - a_i\geq 2$.

On peut démontrer les propriétés suivantes par récurrence, valables tant que la boucle ne s'arrête pas.

$\forall i,\,\, \texttt{l}[a_i] \leq e \leq \texttt{l}[b_i]$
$\forall i,\,\, a_i \leq b_i$

Démonstration par récurrence : L'initialisation est évidente. Soit $i\in\N$. On suppose $a_i \leq b_i$.

On veut montrer que $c_{i+1} \in [a_i,b_i]$. On a $c_{i+1} = \lfloor \frac{a_i+b_i}{2}\rfloor$ et $\frac{a_i+b_i}{2} \in [a_i,b_i]$, donc $c_{i+1}\leq b_i$. Et d'autre part, comme $a_i$ est un entier, on a également $\lfloor \frac{a_i+b_i}{2}\rfloor \geq a_i$.

Dans les deux cas possibles (selon si $\texttt{l}[c_{i+1}]\lt e$ ou non), on a bien $a_{i+1}\leq b_{i+1}$.
$\forall i,\,\, |b_{i+1}- a_{i+1}| \leq \frac{|b_i - a_i|}{2} + \frac{1}{2}. \qquad (*)$

En particulier, comme $|b_i -a_i|\geq 2$, cela implique $$\forall i,\,\,|b_{i+1}-a_{i+1}|\lt |b_i - a_i|. \qquad (\sharp)$$

Justifier la relation $(*)$.

3.3.3. Propriétés de correction et complexité

Terminaison

Justifier la terminaison d'un algorithme signifie justifier que l'algorithme s'arrête forcément.

Ici, il faut justifier que la boucle while ne peut pas boucler indéfiniment. Pour ce faire, on explicite une suite d'entiers qui décroît strictement à chaque itération de la boucle.

D'après $(\sharp)$, tant que la boucle continue, la quantité $|b_i - a_i|$ est strictement décroissante. Comme c'est bien une suite d'entiers positifs, la terminaison est justifiée.

Correction

Les propriétés 1. et 2. justifient la correction de l'algorithme. Quand la boucle s'arrête, on a $\texttt{l}[a_i]\leq e\leq \texttt{l}[b_i]$, $a_i \leq b_i$ et $|b_i - a_i|\leq 1$, donc pour savoir si $e$ appartient à $\texttt{l}$, il suffit de vérifier si $e = \texttt{l}[a_i]$ ou $e = \texttt{l}[b_i]$.

Complexité

Une étude de l'inégalité de récurrence $(*)$ montre que $\forall i,\, |b_i - a_i|\leq \frac{|b_0 - a_0|}{2^i} + 1 = \frac{n-1}{2^i} + 1$

Pour $i = \log_2(n)$, on aurait $|b_i - a_i| \lt 2$, donc l'algorithme s'arrête après au plus $\log_2(n)$ itérations de la boucle.

4. Exercices

4.1. Sur les tris

Écrire une fonction qui prend en argument une liste de flottants et renvoie la valeur absolue de la différence entre les deux valeurs de la liste qui sont les plus proches (en valeur).

Par exemple, si l = [1.2, 4.0, 0.9, 2.3], on renverra 0.3, puisque $|1,2 - 0,9| = 0,3$.

On pourra librement utiliser la fonction sorted.

Écrire une fonction tri_comptage qui prend en argument une liste l dont les éléments sont des entiers de $\db{0,9}$ et qui renvoie une nouvelle liste, contenant les mêmes éléments que la liste l, mais triée.

On procédera en comptant, pour chaque $e\in\db{0,9}$, le nombre de fois que l contient $e$.

On veut une complexité linéaire en la longueur $n$ de la liste, et si possible de l'ordre de $n$ opérations, plutôt que $10 n$.

Essayez : occurrencesplus_communinverse_couplesk_plus_communs

On peut montrer que la complexité moyenne optimale d'un algorithme de tri générique est en $O(n\ln n)$. L'algorithme de l'exercice précédent a une meilleure complexité, mais ne fonctionne que parce que la liste a un nombre fixé d'éléments différents.

Écrire une fonction occurrences qui prend en argument une liste l triée et qui renvoie une nouvelle liste, dont les éléments sont tous les couples $(e, c)$, où $e$ est un élément de la liste l, et $c$ est le nombre de fois qu'il apparaît dans la liste.

Par exemple assert(occurrences([1,1,1,4,4,5,7,7,7,7]) == [(1, 3), (4, 2), (5, 1), (7, 4)]).
En utilisant la fonction précédente et la fonction sorted de Python, écrire une fonction plus_commun qui prend en argument une liste l d'entiers, et renvoie un élément de l qui apparaît le plus de fois.
Écrire une fonction inverse_couples qui prend en argument une liste de couple $(\a_i,\b_i)$, et renvoie la liste des couples $(\b_i, \a_i)$.

On pourra éventuellement proposer une solution d'une ligne, en utilisant la syntaxe de création de liste par extension.
Écrire une fonction k_plus_communs qui prend en argument un entier $k$ et une liste d'entiers et qui renvoie une liste contenant les $k$ éléments (au plus) de la liste l qui apparaissent le plus souvent, du plus courant au moins courant.

On utilisera les questions précédentes, et la fonction sorted, cf remarque suivante.

On peut utiliser la fonction sorted sur une liste de couples, qui sont alors triés par ordre lexicographique, c'est-à-dire suivant la première coordonnée, et, à premières coordonnées égales, suivant la seconde.

assert(sorted([(3, 5), (1,7), (2, 3), (2, 1)]) == [(1,7), (2, 1), (2,3), (3, 5)])

Étant donné deux tableaux triés t1 et t2 de même longueur n, déterminer une médiane de la réunion des deux tableaux en un temps linéaire.

On peut faire mieux, cf l'exercice 4.2.

Alice est professionnellement très demandée.

Écrire une fonction compatible qui prend en argument une liste de couples de flottants $(x_i,y_i)$, avec $x_i \lt y_i$ qui représentent les horaires de début et fin de réunions et qui renvoie True si toutes les réunions sont compatibles. ★ Proposer une solution avec une complexité en $O(n\ln n)$.
Alice veut faire une sieste la plus longue possible. Écrire une fonction sieste_maximale qui prend en argument la même liste que précédemment et qui renvoie la longueur de la plus longue période sans réunion. On veut une complexité en $O(n\ln n)$.

4.2. Recherche dichotomique

Un entier $n\in\N^*$ est appelé une puissance parfaite s'il existe $a\in\N^*$ et $b\geq 2$ tels que $n = a^b$.

Écrire une fonction est_puissance_k qui prend en argument deux entiers $n\geq 1$ et $k\geq 2$ et renvoie True si et seulement si $n$ est une puissance $k$-ième.

On veut une complexité logarithmique.
Écrire une fonction est_puissance_parfaite qui prend en argument un entier $n\geq 1$ et renvoie True si et seulement si $n$ est une puissance parfaite.

On veut une complexité en $O\Big((\ln n)^2\Big)$.

On dispose de deux tableaux d’entiers u et v triés par ordre croissant. Comment déterminer efficacement la valeur qui se trouverait à l’indice $i$ du tableau w que l’on obtiendrait en fusionnant u et v de manière à obtenir un tableau croissant ?¹

d'un zéro d'une fonction continue

Si $f$ est une fonction continue sur un segment $[a,b]$ et vérifie $f(a) f(b)\lt 0$, il existe $c\in [a,b]$ tel que $f(c) = 0$.

Écrire une fonction zero_approch qui prend quatre arguments a, b, f, eps, où a < b sont des flottants, f est une fonction telle que $f(a)\lt 0$, $f(b)\gt 0$ et eps est un flottant $\gt 0$ et qui renvoie un flottant c qui soit une valeur approchée à $\eps$ près d'un zéro de $f$. On procédera par dichotomie. ²
Utiliser la fonction zero_approch pour déterminer une valeur approchée de $\sqrt{2}$ à $10^{-10}$ près, sans utiliser la fonction math.sqrt.
Si $a = 0$ et $b = 1$, quel est, en fonction de $\eps$, le nombre d'itérations de la boucle while nécessaires ?

L'approche dichomotique d'approximation de $\sqrt{2}$ nécessite $-\ln_2(\eps)$ itérations. L'algorithme de Héron permet de le faire en $\ln_2(-\ln_2(\eps))$ itérations.

Un immeuble est constitué de $n$ étages, et l'on possède $m$ assiettes. On souhaite déterminer à partir de quel étage lâcher une assiette par la fenêtre la casse, par des essais successifs. On suppose que si elle ne se casse pas à un essai, on peut descendre récupérer l'assiette et la réutiliser.

Si $m = 1$, quel est le nombre minimal $N_{n,m}$ de lâchers nécessaires pour trouver la réponse dans le pire des cas ? Et si $m = n$ ?
On suppose $m = 2$.
1. Décrire un algorithme avec $O(\sqrt{n})$ lâchers.
2. Déterminer $N_{100, 2}$.³
Écrire une fonction récursive qui calcule $N_{n,m}$.

Notes de bas de page:

On veut une complexité en $\ln \min (|u|, |v|)$.

Indication : utiliser deux variables c, d qui représentent les extrémités de l'intervalle dans lequel se trouve un zéro, et une boucle while

Le résultat est $\lt 19$.